引言
- 在23年电赛对于绕杆巡线代码编写时,姿态函数出现大量四元数相关参数,所以这里做一个较为完整的理论学习。
坐标系的引入
为研究飞行器的姿态,我们一般会在特定的坐标系中描述。一般情况下,分析飞行器运动特性经常要用到以下几种坐标系:1、大地坐标系统;2、地心固定坐标系统;3、本地北东地坐标系统;4、机载北东地坐标系统;5、机体轴坐标系统。
其中3、4、5都是我们建模、设计控制律时经常使用的坐标系,描述物体(刚体)位姿信息的6个自由度信息都是在这三个坐标系中产生的。
首先,机体轴坐标系的原点固连于飞行器重心,X轴指向机头,Z轴指向机腹,X轴和Z轴都位于纵向对称面内,而Y轴指向机身右侧,与X、Z轴构成右手系,该坐标系我们用body的首字母b表示。这就是我们平时control_Position.hpp中相对当前坐标且偏移在Bodyheading系下的含义。
旋转关系
- 目前为止,描述清楚姿态信息的方式有三种:欧拉角、旋转矩阵、四元数。
欧拉角
- 欧拉角是欧拉引入用来描述刚体姿态的三个角,也是我们平常最容易理解,最容易具象表述清楚的一种方式。

- 欧拉角是一种将三维旋转描述为三个连续的旋转的表示方法,分别是绕x轴的旋转、绕y轴的旋转和绕z轴的旋转。比如之后我们将用(z,y,x)顺序来演示万向锁的情况发生。
欧拉角与万向锁
跟据zyx的旋转顺序,
- 绕z轴旋转对应的就是飞行器的偏航运动。

- 绕x轴旋转对应的就是飞行器的横滚运动。

- 绕y轴旋转对应的就是飞行器的俯仰运动。

- 所以我们的飞机俯仰角到达±90°时,你会发现此时绿色代表的滚转运动和蓝色代表的偏航运动他们的旋转轴重合了,这时候你必须要改变最里面自转轴的角度才能够达到你需要的空间位置,而这是违背陀螺定轴性规律的,所以下图陀螺仪中运动的那个方向其实是被锁住了的,你在俯仰角达到±90°时就不可能有这个方向的运动,这是因为当你俯仰角达到±90°时,你改变了第三个要旋转的轴的方向,它与你第一次旋转的Z轴重合了,所以在空间中失去了一个自由度。
(可以随拿个杯子什么的实验一下理解了)
总结:万向锁现象是欧拉角表征姿态的一个固有缺陷,所以,在进行姿态解算时往往会优先使用四元数方法进行描述。
旋转矩阵
- 旋转矩阵反映的了一个坐标在另一个坐标中表示的转换关系。
- 而我们上面描述的三个旋转虽然在三维笛卡尔直角坐标系下进行,但都是平面旋转,他们的旋转矩阵分别是:

所以,从机载NED坐标系到机体轴坐标系的欧拉转换矩阵是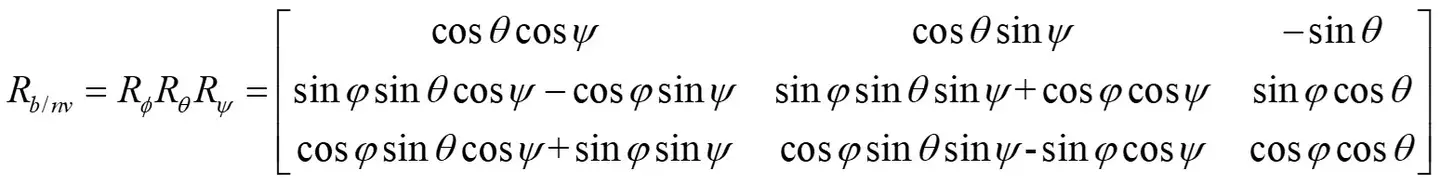
- 根据上图我们就可以很显然的看出,只要θ≠±90°,欧拉角可以描述清楚任何刚体的姿态以及角运动信息,而对于大部分飞行器来说,俯仰角也不会到90°,所以,使用欧拉角进行姿态控制完全可以满足使用要求,但对于一些要求变态机动能力的飞行器来说,为了防止俯仰角90°时出现奇点,使用四元数替代欧拉角进行姿态控制是必须的,另外,对于姿态解算时欧拉角描述方法也会出现问题,所以使用四元数进行姿态解算也是上上之策。
四元数
- 一种数学对象,作为扩展复数的概念。由一个实数和三个虚部构成。没有奇点,能表征任何旋转关系,而且表示简单,只有四个元素,计算量小,但是较不直观,这里知道这个数学知识就行。
通常用以下形式表示:q = a + bi + ci + di - 在计算机图形学中,四元数广泛应用于旋转和插值。由于四元数可以更高效地表示旋转,因此被广泛用作旋转的表示方式,尤其是在三维计算机图形学中。此外,四元数还可以用于执行插值操作,例如在动画和相机路径中进行平滑插值。
- 我们只需要知道四元数这么写可以用来表征姿态,其实是表征旋转关系,跟旋转矩阵的表示方法类似,只不过它只需要4个元素,而旋转矩阵需要9个元素。
实际运用
- 在无人机控制中,四元数常作为飞行器的姿态(也就是飞行器在三维空间中的朝向)
- 在无人机的姿态控制中,需要根据传感器数据(如陀螺仪、加速度计等)来估算飞行器的姿态,并根据期望的姿态来控制飞行器的姿态调整。四元数可以用来表示飞行器的姿态和期望的姿态,通过将其转换为旋转矩阵或欧拉角,实现姿态控制。
- 与传统的欧拉角相比,可以避免万向锁问题。



